INECUACIONES

  

  INECUACIÓN

•  En matemática, una inecuación es una desigualdad algebraica en la que aparecen una o más incógnitas en los miembros de la desigualdad.

•  Si la desigualdad es del tipo  o 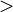 se denomina inecuación en sentido estricto y si es del tipo ≤ o ≥ se denomina inecuación en sentido amplio.

• Del mismo modo en que se hace la diferencia de igualdad y ecuación, una inecuación que es válida para todas las variables se llama inecuación incondicional y las que son válidas solo para algunos valores de las variables se conocen como inecuaciones condicionales.⁴ Los valores que verifican la desigualdad, son sus soluciones.

 Ejemplo de inecuación incondicional: .

• Ejemplo de inecuación condicional: .

                   CLASIFICACIÓN

 Los criterios más comunes de clasificación del ejemplo: .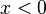

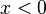• • De dos incógnitas. Ejemplo: .
  • De tres incógnitas. Ejemplo: .
  • etc.

• Según la potencia de la incógnita,
  • De primer grado o lineal. Cuando el mayor exponente de la incógnita de la inecuación es uno. Ejemplo: .
  • De segundo grado o cuadrática. Cuando el mayor exponente de cualquiera de sus incógnitas es dos. Ejemplo: .
  • De tercer grado o cúbica. Cuando el mayor exponente de cualquiera de sus incógnitas es tres. Ejemplo: .
  • etc.

Nota: estas clasificaciones no son mutuamente excluyentes, como se muestra en el último ejemplo.